Code.org does a wonderful job in building the progression of student understanding. For example, in the standard and screen-shot below, students must understand that squares are made up of 4 equal sides and 90-degree angles in order to correctly complete puzzles 1-3.
This lesson also touches on 4.MD.6 Measure angles in whole-number degrees using a protractor. Sketch angles of specified measure.
Teachers should also point out that in puzzle 4, the repeat block is just like repeated addition, which is the same as multiplication. In this case...
Repeated Addition Multiplication
move forward by 100 pixels move forward by 100 pixels
turn right by 90 degrees turn right by 90 degrees
+ x 4
move forward by 100 pixels
turn right by 90 degrees
+
move forward by 100 pixels
turn right by 90 degrees
turn right by 90 degrees
+
move forward by 100 pixels
turn right by 90 degrees
turn right by 90 degrees
4.MD.5.a An angle is measured with reference to a circle with its center at the common endpoint of the rays, by considering the fraction of the circular arc between the points where the two rays intersect the circle. An angle that turns through 1/360 of a circle is called a "one-degree angle," and can be used to measure angles.
4.MD.5.b Define an n-degree angle as n 1-degree angles
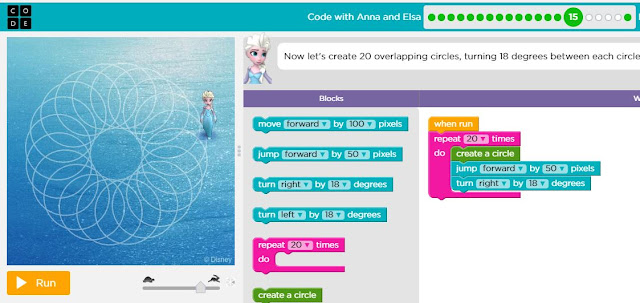
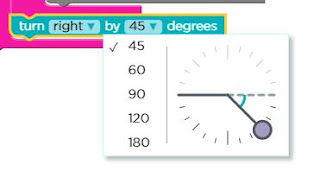
In each puzzle, students are provided with a protractor-type display that helps students determine which angle they may need to solve the puzzle.
THEN...they can explore...
4.MD.7 Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts. Solve addition and subtraction problems to find unknown angles on a diagram in real world and mathematical problems, e.g., by using an equation with a symbol for the unknown angle measure.
In the measurement of angles, a composition is the joining of two angles as sums and is coded as addition. Likewise, decomposition describes the comparison of the measures (m) of two angles and is coded as subtraction. That is, for any angle <ABD located within
<ABC, m<ABD + m<DBC = m<ABC and m<ABC - m<ABD = m<DBC.
Rather than just completing a worksheet on 'missing angles', I would suggest 4th-grade teachers also use Code.org's "Code with Anna and Elsa." Students must find the measure of the angles that will add up to a complete circle = 360-degrees. It is important that an inquiry model of instruction is used, and Code.org suggests 'paired-programming' in which two students work together to complete the puzzles. In puzzle 8 below, students will more than likely use a trial-and-error method when determining that ten lines need to be etched in the ice. Therefore, each angle must be 36-degrees.
For those who have purchased No Fear Coding: Computational Thinking Across the K-5 Curriculum






No comments:
Post a Comment